Se dice que una matriz A es cuadrada si tiene el mismo número de filas que de columnas. ejemplo:
Matriz Rectangular

Es aquella matriz que no es cuadrada, esto es que la cantidad de filas es diferente de la cantidad de columnas.

Matriz Vertical
Es aquella que tiene más filas que columnas.
Matriz Columna
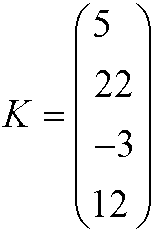
Caso especial de matriz vertical que posee una sola columna.
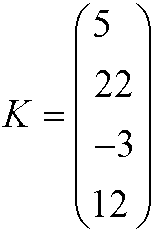
Matriz Horizontal
Es aquella que tiene más columna que filas.
Es aquella que tiene más columna que filas.

Matriz Fila
Caso especial de matriz horizontal que posee una sola fila.
Caso especial de matriz horizontal que posee una sola fila.

Matriz Diagonal
Es una matriz cuadrada en que las entradas o valores son todos nulas salvo en la diagonal principal, otra forma de decirlo es que es diagonal si todos sus elementos son nulos salvo algunos de la diagonal principal.
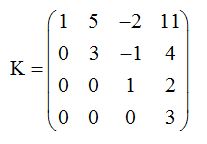

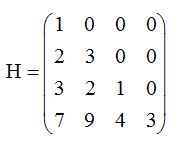



Es una matriz cuadrada en que las entradas o valores son todos nulas salvo en la diagonal principal, otra forma de decirlo es que es diagonal si todos sus elementos son nulos salvo algunos de la diagonal principal.
Matriz Escalonada
Es toda matriz en la que el número de ceros que precede al primer elemento no nulo, de cada fila o de cada columna, es mayor que el de la precedente, puede ser escalonada por filas o escalonadas por columnas.
Es toda matriz en la que el número de ceros que precede al primer elemento no nulo, de cada fila o de cada columna, es mayor que el de la precedente, puede ser escalonada por filas o escalonadas por columnas.
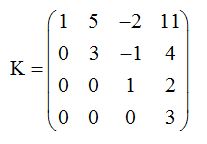
Matriz Triangular Superior
Se dice una matriz (cuadrada) es triangular superior si todos los elementos que están por debajo de la diagonal principal son nulos.
Se dice una matriz (cuadrada) es triangular superior si todos los elementos que están por debajo de la diagonal principal son nulos.

Matriz Triangular Inferior
Se dice que una matriz es triangular inferior si todos los elementos que están por encima de la diagonal principal son ceros.
Se dice que una matriz es triangular inferior si todos los elementos que están por encima de la diagonal principal son ceros.
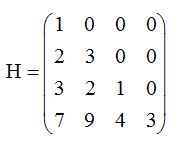
Matriz Identidad
Se llama matriz identidad de orden n y se nota I-n a una matriz cuadrada de orden n en la que los elementos de la diagonal principal son 1 y el resto 0.
Se llama matriz identidad de orden n y se nota I-n a una matriz cuadrada de orden n en la que los elementos de la diagonal principal son 1 y el resto 0.
Matriz Nula o Matriz Cero
Es una matriz con todos sus elementos nulos, o sea de valor cero.
Es una matriz con todos sus elementos nulos, o sea de valor cero.
Matriz Opuesta
Teniendo una matriz determinada, se llama matriz opuesta de la antes mencionada a aquella que tiene por elementos los opuestos de los elementos de la matriz original.
Teniendo una matriz determinada, se llama matriz opuesta de la antes mencionada a aquella que tiene por elementos los opuestos de los elementos de la matriz original.

Matriz Transpuesta
Matriz transpuesta (At). Se llama matriz transpuesta de una matriz A a aquella matriz cuyas filas coinciden con las columnas de A y las columnas coinciden con las filas A.
Matriz transpuesta (At). Se llama matriz transpuesta de una matriz A a aquella matriz cuyas filas coinciden con las columnas de A y las columnas coinciden con las filas A.
Matriz Simétrica
Una matriz es simétrica cuando es una matriz cuadrada, y es igual a su transpuesta.
Una matriz es simétrica cuando es una matriz cuadrada, y es igual a su transpuesta.

Matriz Antisimétrica
Una matriz es antisimétrica cuando es una matriz cuadrada, y es igual a su transpuesta de signo opuesto, siendo los elementos de la diagonal principal nulos, de valor cero.
Una matriz es antisimétrica cuando es una matriz cuadrada, y es igual a su transpuesta de signo opuesto, siendo los elementos de la diagonal principal nulos, de valor cero.

Matriz Ortogonal
Una matriz ortogonal es una matriz cuya matriz inversa coincide con su matriz traspuesta.

Matriz Normal
Sea A matriz compleja cuadrada, entonces es una matriz normal si y solo si A*A= AA* donde A* es la matriz transpuesta conjugada de A (también llamado hermitiano).

Matriz Conjugada
Una matriz conjugada es el resultado de la situación de los elementos de una matriz A por sus valores conjugados. Es decir, la parte imaginaria de los elementos de la matriz cambian sus signos.

Matriz Invertible
Una matriz ortogonal es una matriz cuya matriz inversa coincide con su matriz traspuesta.

Matriz Normal
Sea A matriz compleja cuadrada, entonces es una matriz normal si y solo si A*A= AA* donde A* es la matriz transpuesta conjugada de A (también llamado hermitiano).

Matriz Conjugada
Una matriz conjugada es el resultado de la situación de los elementos de una matriz A por sus valores conjugados. Es decir, la parte imaginaria de los elementos de la matriz cambian sus signos.

Matriz Invertible
También llamada matriz, no singular, no degenerada, regular. Una matriz cuadrada A de orden n se dice que es invertible si existe otra matriz cuadrada de orden n, llamada matriz inversa de A y representada como A-1, tal que AA-1= A-1 A= In1 bl donde In es la matriz identidad de orden n y el producto de matrices usual. Una matriz tiene inversa siempre que su determinante no sea cero. La inversión de matrices es el proceso de encontrar la matriz inversa de una matriz dada.


Matriz Singular o Degenerada
También llamada no regular. Una matriz es singular si y solo si su determinante es cero.
Matriz Permutación
La matriz permutación es la matriz cuadrada con todos sus nxn elementos iguales a 0, excepto uno cualquiera por cada fila y columna, el cual debe ser igual a 1.

Matrices Iguales
Se dice que dos matrices A y B son iguales si tienen la misma dimension y son iguales elemento a elemento, es decir, aij=bij i=1,2......,m.

Matriz Hermitiana
Una matriz hermitiana o (hermitica) es una matriz cuadrada de elementos complejos que tiene la caracteristica de ser igual a su propia transpuesta conjugada. es decir, el elemento en la i-ésima fila y i-ésima columna es igual al conjugado del elemento en la j-ésima fila e i-ésima columna, para todos los indices i y j.

Matriz Definida Positiva
Una matriz definida positiva es una matriz hermitiana que en muchos aspectos es similar a un número real positivo.
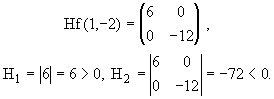
Matriz Unitaria

Submatriz
A partir de una matriz M, se llama submatriz M´ a toda matriz obtenida suprimiendo p filas y q columnas en M. Si M es de orden mxn. M´ será a toda matriz obtenida suprimiendo p filas menos y q columnas menos. Es evidente que p < m; 1<n.

Matriz Permutación
La matriz permutación es la matriz cuadrada con todos sus nxn elementos iguales a 0, excepto uno cualquiera por cada fila y columna, el cual debe ser igual a 1.
Matrices Iguales
Se dice que dos matrices A y B son iguales si tienen la misma dimension y son iguales elemento a elemento, es decir, aij=bij i=1,2......,m.

Matriz Hermitiana
Una matriz hermitiana o (hermitica) es una matriz cuadrada de elementos complejos que tiene la caracteristica de ser igual a su propia transpuesta conjugada. es decir, el elemento en la i-ésima fila y i-ésima columna es igual al conjugado del elemento en la j-ésima fila e i-ésima columna, para todos los indices i y j.

Matriz Definida Positiva
Una matriz definida positiva es una matriz hermitiana que en muchos aspectos es similar a un número real positivo.
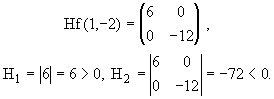
Matriz Unitaria
Es una matriz compleja U, de n por n elementos, que satisface la condición: U*U= UU* = In donde In es la matriz identidad y U* es el transpuesto conjugado (también llamado el hermitiano adjunto o la hermitica) de U. Esta condicion implica que una matriz U es unitaria tiene inversa igual a su transpuesta conjugada U*. Una matriz unitaria e nla que todas las entradas son reales es una matriz ortogonal.

Submatriz
A partir de una matriz M, se llama submatriz M´ a toda matriz obtenida suprimiendo p filas y q columnas en M. Si M es de orden mxn. M´ será a toda matriz obtenida suprimiendo p filas menos y q columnas menos. Es evidente que p < m; 1<n.





No hay comentarios:
Publicar un comentario